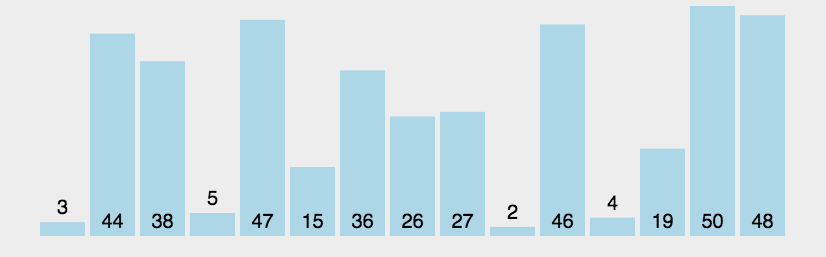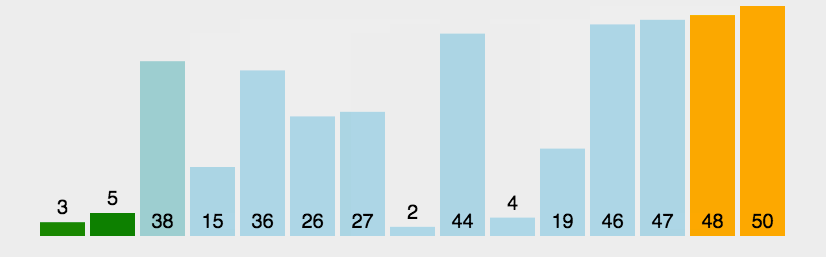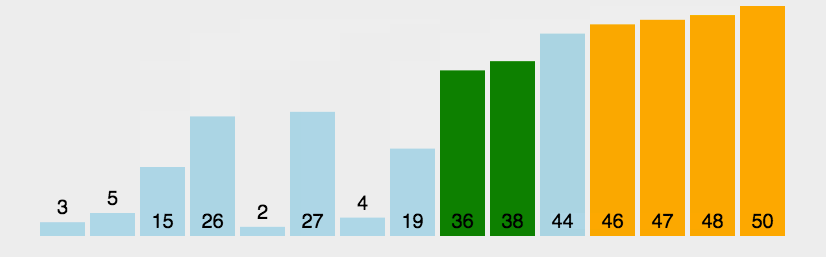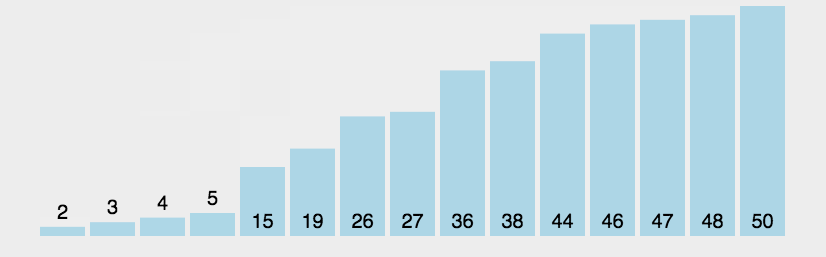
每次提到排序印象都是,学过排序,但脑子里就剩下个快排,抽个空把所有叫得上名字的排序整理下,日后复习起来也简单些。
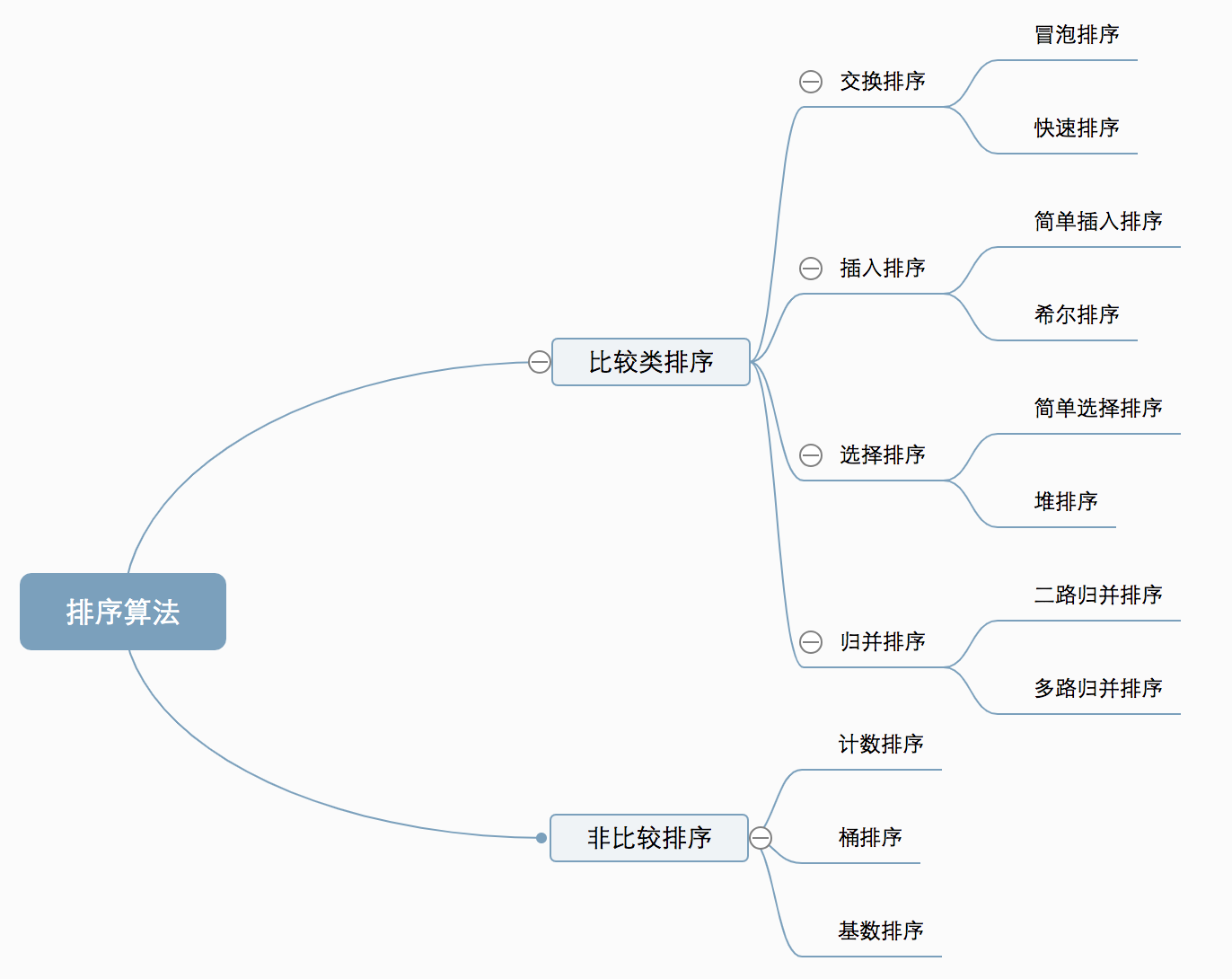
分类
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
基本概念介绍
1 冒泡排序 Bubble Sort
算法描述
比较基本的排序算法,在每次循环开始时从一端的元素开始向另一端循环,遇到右>左则换位,这样在第一遍循环之后 我们可以保证数组的最右端是最大元素。依次重复n此后可保证数组按顺序排列完毕。
动图演示
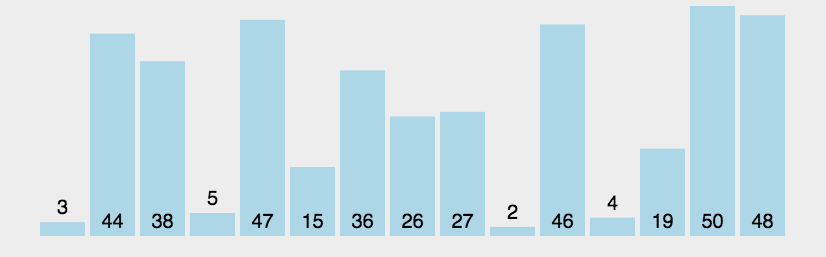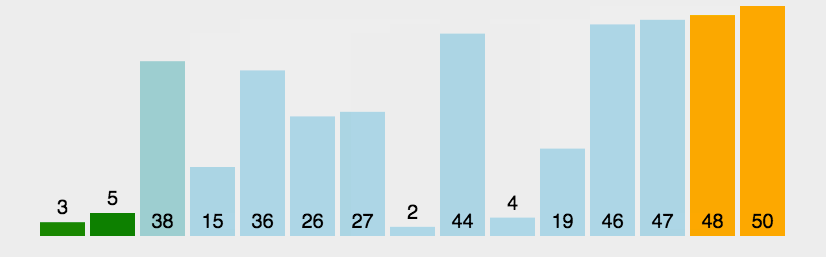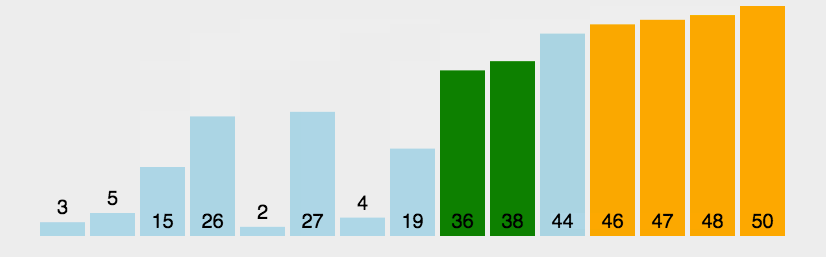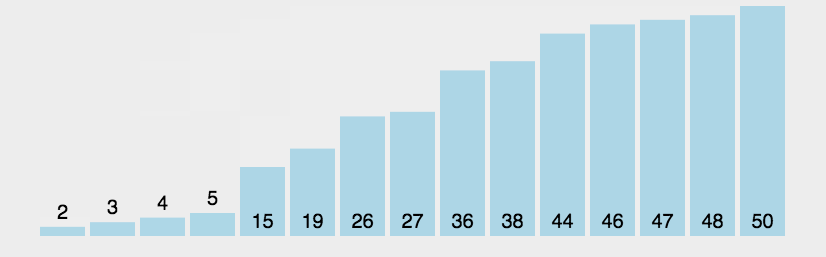
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void bubbleSort(int* arr,int len){
int value;
for(int i = 0;i<len-1;i++){
int* pivot = &arr[i];
for(int index = i+1;index <len ;index++){
if(arr[index]<*pivot){
value = *pivot;
*pivot = arr[index];
pivot = & arr[index];
*pivot = value;
}
}
}
}
|
分析
2 选择排序 Selection Sort
算法描述
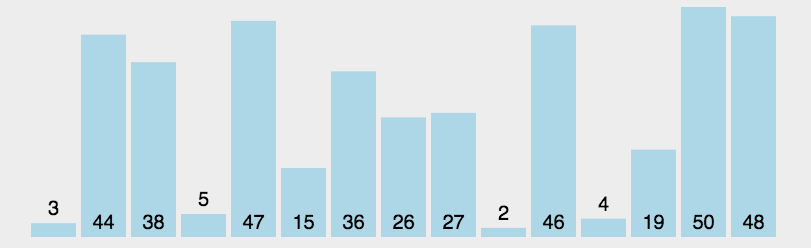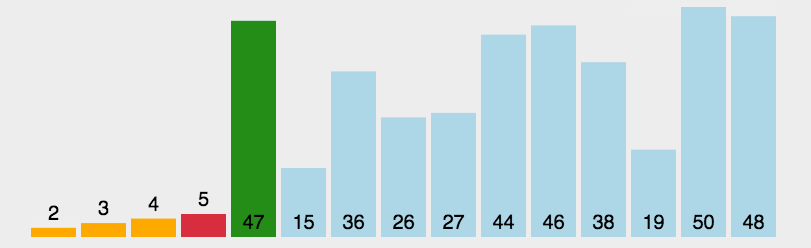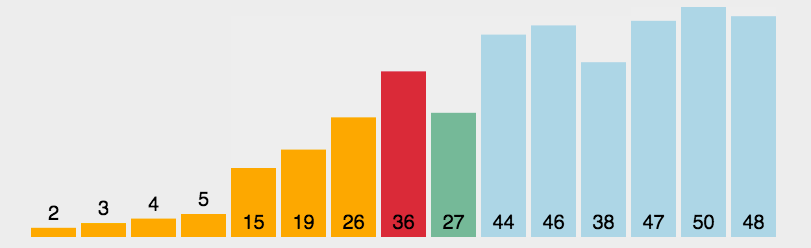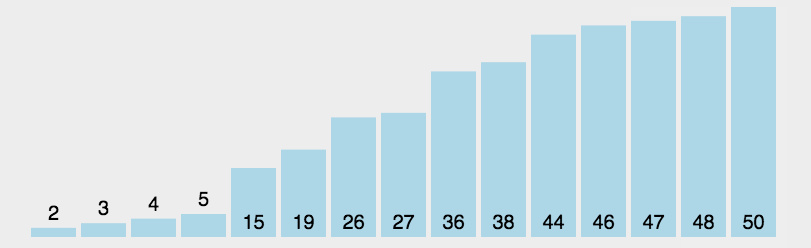
也是一个比较基本的排序算法,每次循环时找到数组中最小的元素将其放在数组最左端。循环n次后得到排序完成的数组。
动图演示
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| void selectionSort(int* arr,int len){
int value;
for(int i = 0;i<len-1;i++){
int* pivot = & arr[i];
for(int index = i+1;index<len;index++){
if(arr[index]<*pivot){
pivot = &arr[index];
}
}
value = *pivot;
*pivot = arr[i];
arr[i] = value;
}
}
|
分析
3 插入排序 Insertion Sort
算法描述
大体思想为,循环i次时,保证数组的前i位元素都为已经排序好的,每次到i元素
动图演示

代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| void selectionSort(int* arr,int len){
int value;
for(int i = 0;i<len-1;i++){
int* pivot = & arr[i];
for(int index = i+1;index<len;index++){
if(arr[index]<*pivot){
pivot = &arr[index];
}
}
value = *pivot;
*pivot = arr[i];
arr[i] = value;
}
}
|
分析
4 希尔排序 Shell Sort
算法描述
1959年Shell发明,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行k 趟排序;(不同颜色表示不同序列 )
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
动图演示
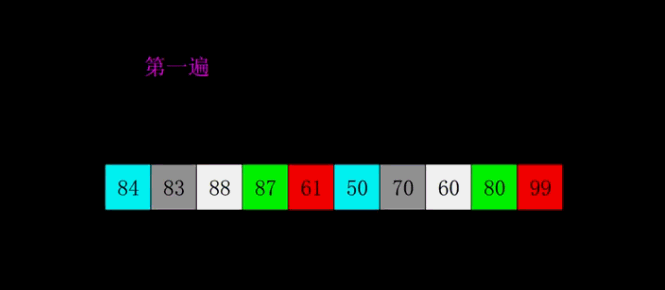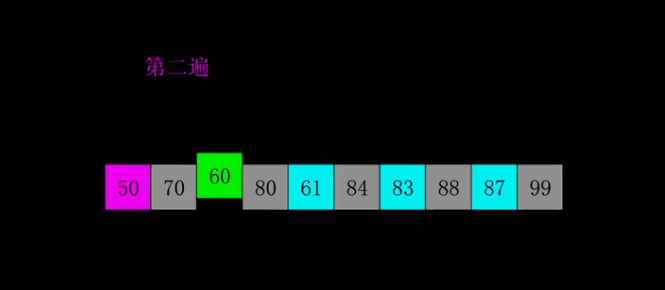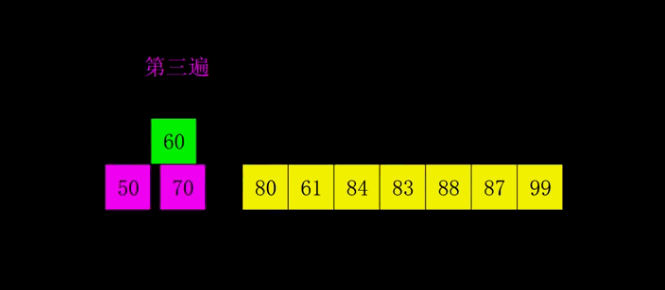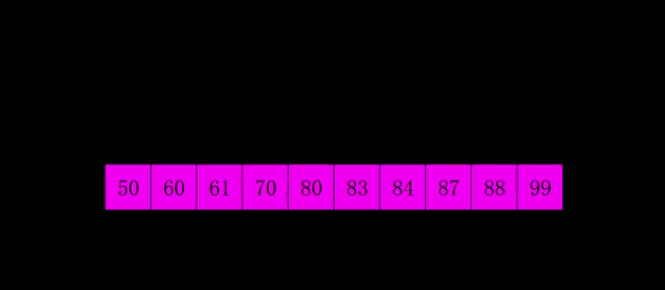
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| function shellSort(arr) {
varlen = arr.length;
for(vargap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
for(vari = gap; i < len; i++) {
varj = i;
varcurrent = arr[i];
while(j - gap >= 0 && current < arr[j - gap]) {
arr[j] = arr[j - gap];
j = j - gap;
}
arr[j] = current;
}
}
returnarr;
}
|
分析
5 归并排序 Merge Sort
算法描述
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
动图演示
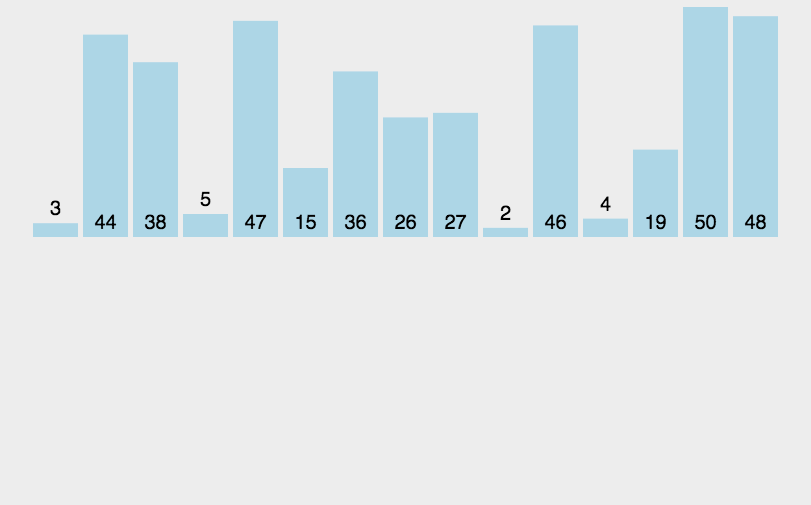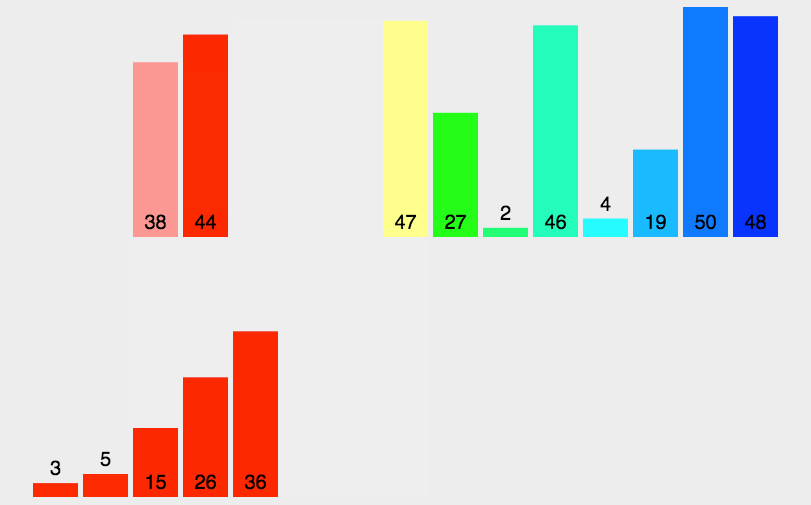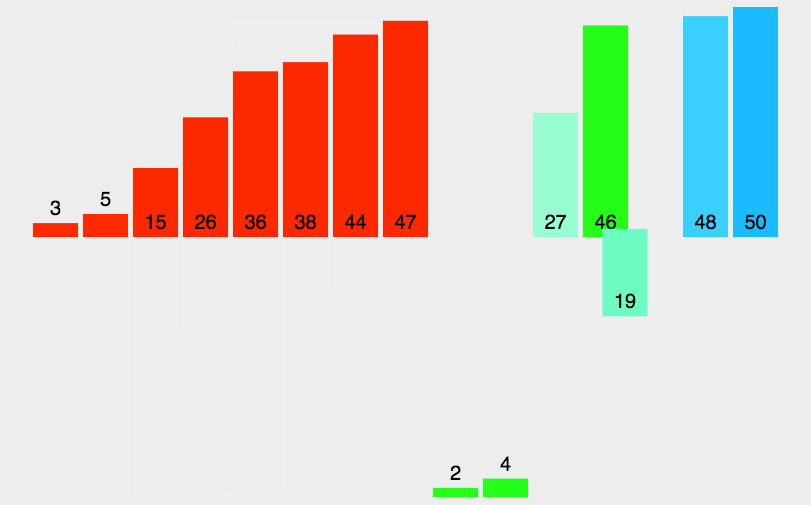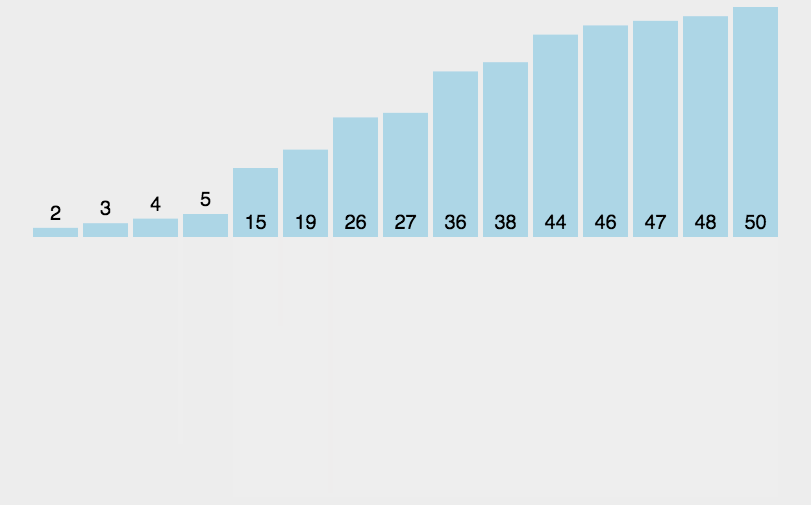
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| function mergeSort(arr) {
varlen = arr.length;
if(len < 2) {
returnarr;
}
varmiddle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle);
returnmerge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
varresult = [];
while(left.length>0 && right.length>0) {
if(left[0] <= right[0]) {
result.push(left.shift());
}else{
result.push(right.shift());
}
}
while(left.length)
result.push(left.shift());
while(right.length)
result.push(right.shift());
returnresult;
}
|
分析
6 快速排序 Quick Sort
算法描述
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
动图演示

代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| function quickSort(arr, left, right) {
varlen = arr.length,
partitionIndex,
left =typeofleft !='number'? 0 : left,
right =typeofright !='number'? len - 1 : right;
if(left < right) {
partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex-1);
quickSort(arr, partitionIndex+1, right);
}
returnarr;
}
function partition(arr, left ,right) {
varpivot = left,
index = pivot + 1;
for(vari = index; i <= right; i++) {
if(arr[i] < arr[pivot]) {
swap(arr, i, index);
index++;
}
}
swap(arr, pivot, index - 1);
returnindex-1;
}
function swap(arr, i, j) {
vartemp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
|
分析
7 堆排序 Heap Sort
算法描述
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
参考博客