大数据与隐私

发表于 更新于 阅读次数： Artalk：

大数据技术在提升社会协作效率、给人们带来诸多便利与舒适的同时, 也逐渐引发了一系列问题, “大数据杀熟”便是恶果之一。

​ 所谓“大数据杀熟”, 通俗说来就是平台(主要是互联网平台)充分利用自身所掌握的大数据技术对消费市场进行更为精准与细腻的划分, 在此基础上主要对熟人(习惯、依赖该平台的较为忠诚的用户)进行不当地利益宰割, 从而使大数据技术成为部分经营者追求超额利润的有力工具。也就是说, 面临同样的商品或服务, 具有忠诚度的用户群体看到并为此实际支付的价格反而比新客户或一般用户要贵, 而且这种行为极具隐蔽性。一言以蔽之, 大数据技术加剧了经营者和相对人之间的的信息不平等, 消费者很难通过网络对经营者价格歧视的抗辩进行甄别

​ 究其本质, “大数据杀熟”的技术原理就是互联网平台凭借其所掌握的极其庞大且维度异常丰富的数据, 诸如用户的个人身份信息、位置信息、聊天记录以及支付信息等一切有可能被线上记录的数字化信息, 然后通过一整套复杂、高效而又极其先进的数据运算、分析和挖掘技术对碎片化、零散的用户数字化信息进行全方位的扫描、分析与研究(数据标注), 然后通过一些关键词的标注对用户进行细致归类, 从而生成独特的 用户画像。

1 主因

1.数据高度集中，互联网的发展建立在用户数据的规模智商，用户规模越大整个互联网越能发挥出更大的效用，综合价值成集合式增长。 相较于传统经济样态, 互联网经济的边际成本非常低, 收益却可以很高,自然导致了数据的集中于垄断。

2.用户”粘性“，用户粘性是各大互联网产品重要的指标。用户长久的习惯于使用某一平台，由于用户对便利、稳定的追求使得有被”杀熟“的可能。

3.不同平台间的隐私窃取。微信与京东，支付宝与淘宝等的相互泄漏数据很易使得用户的偏好或购物倾向被泄漏，从而引导消费、杀熟等。粘贴板、输入法等获取信息。

矛盾：

公司需要用户数据刻画用户画像，以此来提供服务

VS

公民隐私泄漏给互联网公司利用用户隐私数据创造价格歧视的机会

据此，按照通行的观点，价格歧视往往被分为三级：

一级价格歧视，即看人报价，报出对方能够接受的最高价，攫取最大利润；传统商业社会中，游商采用这种方式比较多；

二级价格歧视，即根据批量大小定价，从而获得最好的周转率，批量大的消费者获得实惠；从商家角度看，虽然单一商品获利降低，但由于销量增加，也可以获得更大的利润；

三级价格歧视，是根据销售区域的不同进行差异化定价。

对于大数据杀熟，我国法律中已经有相应的规则进行规范。《中华人民共和国消费者权益保护法》第十九条规定：商店提供商品应明码标价。该法第十条规定：消费者享有公平交易的权利。明码标价意味着商品价格展示不应因为消费者不同而不同，由于不同的消费者看到的价格不同，因而大数据杀熟违反了明码标价的原则。消费者权益保护法规定消费者获得公平交易的权利，也从另一个角度说明了相同商品或服务的定价应一视同仁。

数据安全法，6.10通过

2 数据中个人隐私保护的技术分析

2.1 将id去敏？

例如在用户数据需要被使用时，使用去敏手段，如：将名字等敏感的个人信息去除。

问题： How anonymous ?

2006 netflix收集大量用户评分一次来训练自己的评分预测功能：

1， 将uid改为无意义代码

2，随机修改部分用户评分

Robust De-anonymization of Large Sparse Datasets

(利用了imdb的数据库，correlation 可以)

马萨诸塞州，医疗数据。

考虑彼此反推数据，如何加密？

2.2 只发布粗粒度的统计数据？

 Age  Gender  Employed? <18M Yes <18 F No <18M No ≥18 F Yes ≥18 F Yes  Original dataset \begin{array}{l} \begin{array}{|c|c|c|} \hline \text { Age } & \text { Gender } & \text { Employed? } \\ \hline<18 & \mathrm{M} & \text { Yes } \\ \hline<18 & \mathrm{~F} & \text { No } \\ \hline<18 & \mathrm{M} & \text { No } \\ \hline \geq 18 & \mathrm{~F} & \text { Yes } \\ \hline \geq 18 & \mathrm{~F} & \text { Yes } \\ \hline \end{array}\\ {\text { Original dataset }} \end{array}

 Age  Employed?  Count <18 Yes 1<18 No 2≥18 Yes 2≥18 No 0 Age  Gender  Count <18M2<18 F1≥18M0≥18 F2\begin{array}{l} \begin{array}{|c|c|c|} \hline \text { Age } & \text { Employed? } & \text { Count } \\ \hline<18 & \text { Yes } & 1 \\ \hline<18 & \text { No } & 2 \\ \hline \geq 18 & \text { Yes } & 2 \\ \hline \geq 18 & \text { No } & 0 \\ \hline \end{array}\\ \begin{array}{|c|c|c|} \hline \text { Age } & \text { Gender } & \text { Count } \\ \hline<18 & \mathrm{M} & 2 \\ \hline<18 & \mathrm{~F} & 1 \\ \hline \geq 18 & \mathrm{M} & 0 \\ \hline \geq 18 & \mathrm{~F} & 2 \\ \hline \end{array}\\ \end{array}

很容易可以从发布的两份数据中反推出必有两个大于18岁女性，有工作。

（数据重构攻击）

可能解决方法：

1，对统计结果加上有权重的噪音，处理outlier

2， 统计结果上，将outlier划入相对大的群体，减少outlier

2.3 Deferential Privacy

exp⁡(−ε)≤Pr⁡[A(D)=O]Pr⁡[A(D′)=O]≤exp⁡(ε)\exp (-\varepsilon) \leq \frac{\operatorname{Pr}[A(D)=O]}{\operatorname{Pr}\left[A\left(D^{\prime}\right)=O\right]} \leq \exp (\varepsilon)

对任意“相邻"数据集 DD 和 D′D^{\prime} 及任意输出 OO 都成立

1,拉普拉斯噪声

pdf⁡(x)=12λexp⁡(−∣x∣λ)\operatorname{pdf}(x)=\frac{1}{2 \lambda} \exp \left(-\frac{|x|}{\lambda}\right)

lambda为 相邻数据集查询发生的最大改变量 / ϵ\epsilon

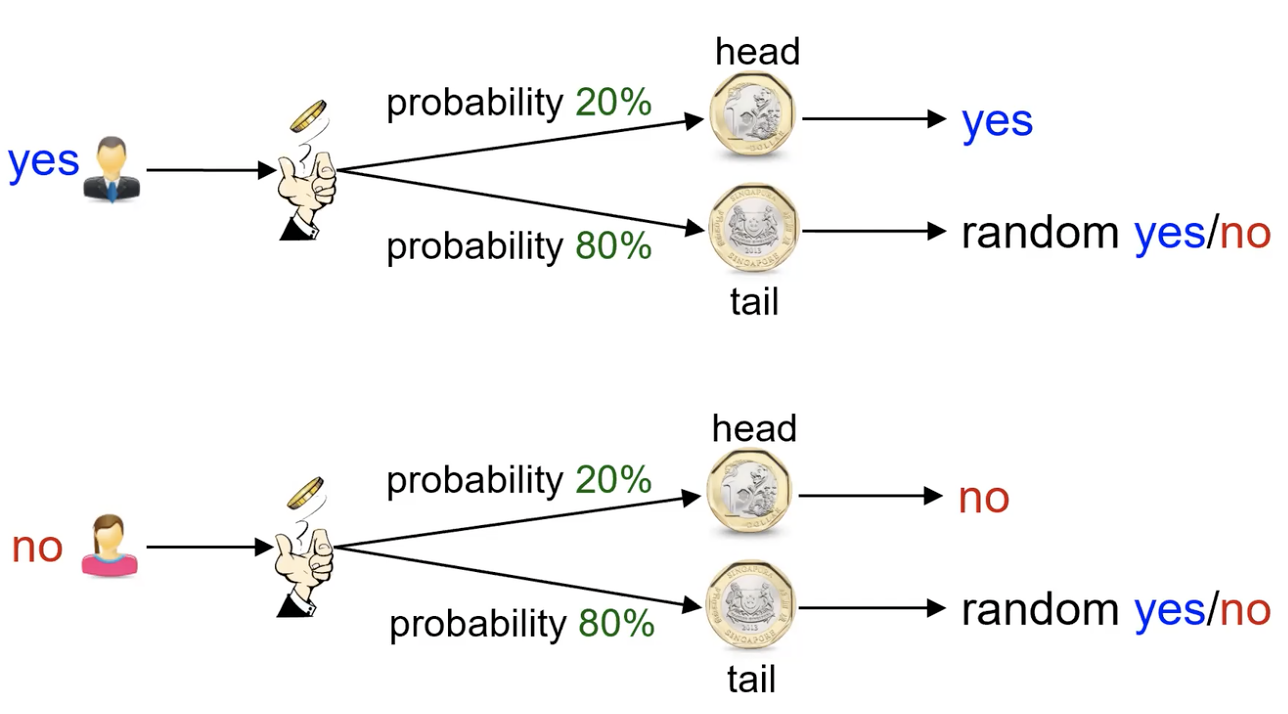
  1. random answer

    引入随机量计入答案，保证统计量依然准确可感。