LP Simplex

发表于 更新于 阅读次数： Artalk：

对linear programming做一个复习note，第一部分从simplex 开始讲起

Recap of LP and BFS

简单的来说，由目标函数、线性约束组成的优化问题就是 Linear Programming, 形如：

min⁡c⊤x s.t. A1x≤b1A2x≥b2x≥0\begin{aligned} \min && \quad & c^{\top} x \\ \text { s.t. } && A_1 x&\leq b_1 \\ && A_2 x&\geq b_2 \\ && x &\geq 0 \end{aligned}

Geometry of LP

每个LP的feasible region都可以表示为一个 polyhedron

Definition:

A polyhedron is a set that can be described in the form

{x∈Rn∣Ax≥b}\left\{\mathbf{x} \in \mathbb{R}^n \mid A \mathbf{x} \geq \mathbf{b}\right\}

where AA is an m×nm \times n matrix and b∈Rm\mathbf{b} \in \mathbb{R}^m.

Standard Form of LP

通过添加slack variable，我们可以简单地把LP问题转化为如下的standard form：

max⁡c⊤x s.t. Ax=bx≥0\begin{aligned} \max && \quad & c^{\top} x \\ \text { s.t. } && A x&=b \\ && x &\geq 0 \end{aligned}

Assumption:

A has linealy independent rows, or equivalently A has full row rank.

Basic Feasible Solution: We call x\mathbf{x} a basic solution \color{red} \text{basic solution }of the LP if and only if

  1. Ax=bA \mathbf{x}=\mathbf{b}
  2. There exist indices B(1),…,B(m)B(1), \ldots, B(m) such that the columns AB(1),…,AB(m)A_{B(1)}, \ldots, A_{B(m)} are linearly independent, and xi=0x_i=0 for i≠B(1),…,B(m)i \neq B(1), \ldots, B(m)

We call x\mathbf{x} a basic feasible solution \color{red} \text{basic feasible solution } if x≥0\mathbf{x}\geq0

  • For the standard LP polyhedron {x:Ax=b,x≥0}\{\mathbf{x}: A \mathbf{x}=\mathbf{b}, \mathbf{x} \geq 0\}, the followings are equivalent:

    • x\mathbf{x} is an extreme point
    • x\mathbf{x} is a basic feasible solution

  • If there is a feasible solution, there is a basic feasible solution;

  • If there is an optimal solution, there is an optimal solution that is a basic feasible solution.

所以为了求解一个LP，我们有一个很直接的做法，遍历所有的BFS找到最优的解

Simplex Method

Simplex method 的roadmap：

  1. 找到任意一个BFS作为启动
    1. 找到一个BFS可能不是那么容易的，可能会涉及2-phase method
  2. 从1个BFS开始把1个顶点踢出basics 把另一个顶点换进basis（需确保这样使objective变好），几何上看我们在做的事情类似于沿着LP Polyhedron的某一条边，从一个顶点移动到另一个顶点
  3. 一直重复上述两步，直到没有相邻的BFS能带来更好的objective value
    1. 需确保不会陷入cycling（Bland' s Rule）

Simplex Method with Dictionary

考虑这样一个example：

maximize−x1+3x2−3x3subject to3x1−x2−2x3≤7−2x1−4x2+4x3≤3x1−2x3≤4−2x1+2x2+x3≤83x1≤5x1,x2,x3≥0.\begin{aligned} & \text{maximize} & -x_1 + 3x_2 - 3x_3 \\ & \text{subject to} & 3x_1 - x_2 - 2x_3 & \leq 7 \\ & & -2x_1 - 4x_2 + 4x_3 & \leq 3 \\ & & x_1 - 2x_3 & \leq 4 \\ & & -2x_1 + 2x_2 + x_3 & \leq 8 \\ & & 3x_1 & \leq 5 \\ & & x_1, x_2, x_3 & \geq 0. \end{aligned}

Rewrite with Slack Variable

maximizeζ=−x1+3x2−3x3subject tow1=7−3x1+x2+2x3w2=3+2x1+4x2−4x3w3=4−x1+2x3w4=8+2x1−2x2−x3w5=5−3x1x,w≥0\begin{aligned} \text{maximize} \quad \zeta & = -x_1 + 3x_2 - 3x_3 \\ \text{subject to} \quad w_1 & = 7 - 3x_1 + x_2 + 2x_3 \\ w_2 & = 3 + 2x_1 + 4x_2 - 4x_3 \\ w_3 & = 4 - x_1 + 2x_3 \\ w_4 & = 8 + 2x_1 - 2x_2 - x_3 \\ w_5 & = 5 - 3x_1 \\ &\mathbf{x}, \mathbf{w} \geq 0 \end{aligned}

  • 通过加入slack variable $\mathbf{w} $可以把不等式转化为等式
  • $\mathbf{w} $需确保>0

第一个BFS很容易得到，我们直接把x\mathbf{x}考虑为0，w\mathbf{w}按约束条件求出来，就得到了第一个BFS，我们写成如下的dictionary表格的形式：

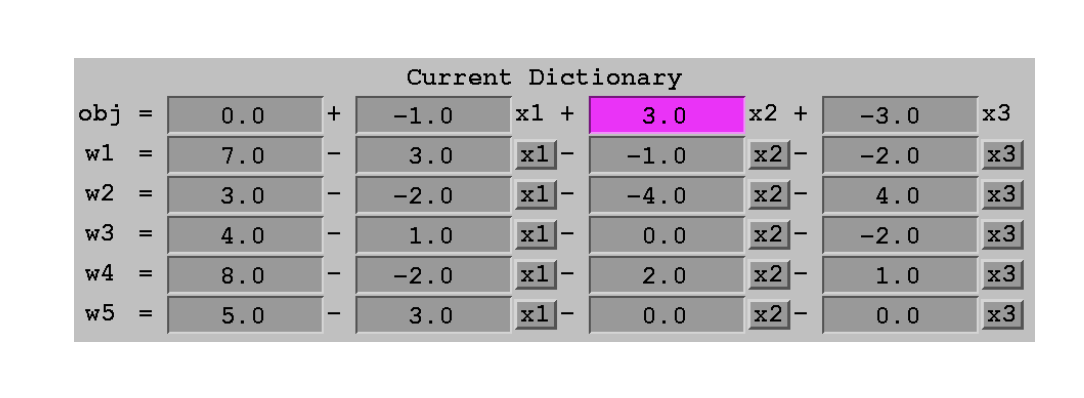
Simplex Method Example
Initial dict

  • 第一行是objective 行，这一行上的variable取0，不在basis里

  • 余下几行（w1-w5）是basis行，他们都在basis里

观察objective行我们可以发现，x2x_2前面的系数是正的，也就意味着如果能把x2x_2 从0 increase 就可以提高obj value，那么最多能提高多少呢？

需要确保现在在basis里的variable 不会因为x2x_2的提高而变为负数,观察余下几行我们会发现x2x_2提高会导致w1-w5变化，那么一直到第一个w变为0我们就该停止提升x2 了，比较发现w4w_4是最先变为0的。因此我们把x2x_2变为非0（放入basis），w4w_4变为0（移出basis）

注意在其他行内也要把w4 替换掉，底下几行只能出现非basis内的变量：

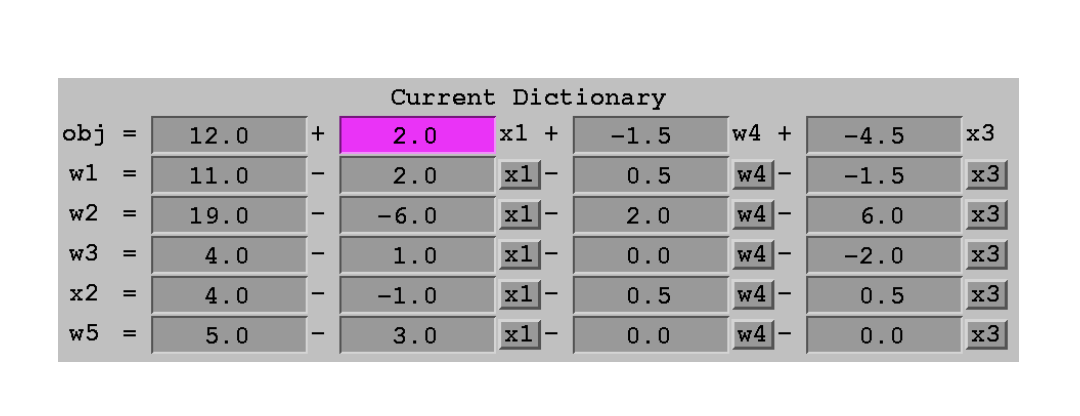
Simplex Method Example
Dict after step 1

下一步做类似的处理，把x1x_1前的系数仍然是正的，增加x1x_1使得w5w_5先到0

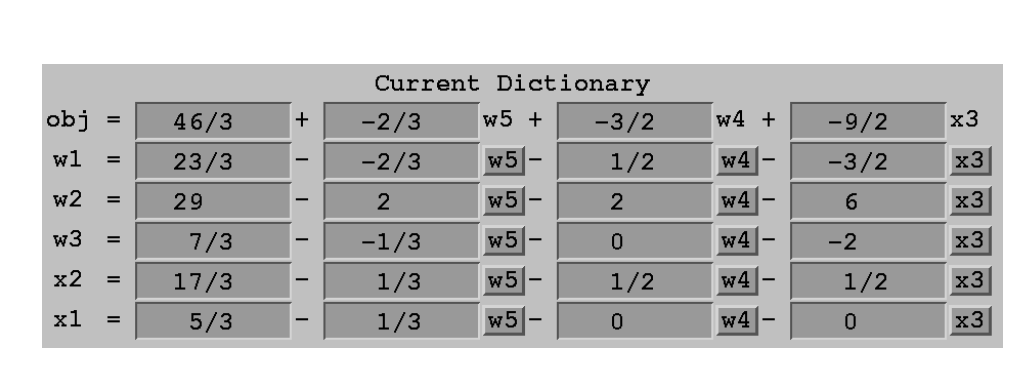
Simplex Method Example
Dict after step 2

此时发现obj中所有的variable都是负数系数。我们得到了最优解！

Potential Pitfalls

我们之前的example规避了几个常见的麻烦：

  1. 我们找initial dictionary时，只需要把x\mathbf{x}设为0，slack variable进入basis，但这是因为这样得到的slack variable都是非负的，如果x=0\mathbf{x}=0时slack variable为0 那么就不是一个合法的BFS。
  2. 如果我们的iteration陷入一个cycling？
  3. 如果我们在找替换basis时发现所有的basis都不会到0反而会到正无穷？（unbounded）

Unboundedness Detection:

考虑这个dictionary：

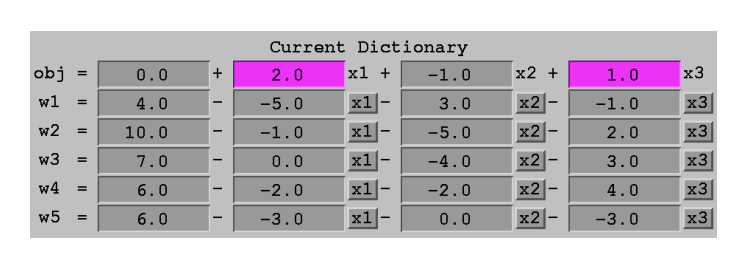
Simplex Method Example
Unbounded Example

我们可以无限制地提高x1x_1,因此这是一个unbounded的问题

Initialization (2-phases)

2-phase method的思想：

x1+1≤0x_1+1\leq0 添加slack 变为 x1+1+w1=0,w1≥0x_1+1+w_1=0, w_1\geq0,但直接令x1=0x_1=0得到的w1w_1是 负数。我们再添加一个辅助变量： x1+1+w1−x0=0,w1≥0,x0≥0x_1+1+w_1-x_0=0, w_1\geq0,x_0\geq0，

此时，我们是能为这个constraint找到一个对应的basis variable x0x_0 的，我们下面做一些操作把x0x_0移出basis得到一个新的BFS（x0=0x_0=0的一个BFS），这个BFS一定也是原问题的BFS。

怎么把移出basis呢？我们很巧妙的定义了一个新的优化问题（Phase-I problem）。

我们用一个例子展示这种思想。

原问题：

\begin{align*} \text{maximize} \quad & -x_0 \\ \text{subject to} \quad & -x_0 - 4x_1 - 2x_2 & \leq -8 \\ & -x_0 - 2x_1 & \leq -2 \\ & -x_0 + 3x_1 + 2x_2 & \leq 10 \\ & -x_0 - x_1 + 3x_2 & \leq 1 \\ & -x_0 - 3x_2 & \leq -2 \\ & x_0, x_1, x_2 & \geq 0. \end{align*}

Phase 1:

  • Modify problem by subtracting a new variable, x0x_0, from each constraint and
  • replacing objective function with −x0-x_0

\begin{align*} \text{maximize} \quad & -x_0 \\ \text{subject to} \quad & -x_0 - 4x_1 - 2x_2 & \leq -8 \\ & -x_0 - 2x_1 & \leq -2 \\ & -x_0 + 3x_1 + 2x_2 & \leq 10 \\ & -x_0 - x_1 + 3x_2 & \leq 1 \\ & -x_0 - 3x_2 & \leq -2 \\ & x_0, x_1, x_2 & \geq 0. \end{align*}

用Simplex method 解这个问题如果：

  • Obj != 0 说明，原问题无解
  • Obj=0，我们得到了一组解其中x0=0x_0=0这组解一定是原问题的一个BFS

Phase 2:

用 Phase 1得到的BFS开始迭代

Cycling Detection

Theorem (Bland's Rule) If we use both the smallest index rule for choosing the entering basis and the exiting basis, then no cycle will occur in the simplex algorithm.

如果有多个variable 可以进入basis(在obj行上的系数为正)也可以离开basis(同时触0)，一个确定的ordering规则可以保证不会出现cycling，最简单直接的就是用index作为order的顺序index。